0 saved
7.2K views
Think back to the last time you overindulged in a huge, delicious dessert. It’s likely that the first bite was divine, but perhaps ...
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Sed quanta sit alias, nunc tantum possitne esse tanta. Videamus animi partes, quarum est conspectus illustrior; Videmus igitur ut conquiescere ne infantes quidem possint. Tu vero, inquam, ducas licet, si sequetur; Prodest, inquit, mihi eo esse animo. Summus dolor plures dies manere non potest? Nonne videmus quanta perturbatio rerum omnium consequatur, quanta confusio? Duo Reges: constructio interrete.
Tecum optime, deinde etiam cum mediocri amico. Compensabatur, inquit, cum summis doloribus laetitia. Aliter homines, aliter philosophos loqui putas oportere? Eiuro, inquit adridens, iniquum, hac quidem de re; Nec vero pietas adversus deos nec quanta iis gratia debeatur sine explicatione naturae intellegi potest. Haec non erant eius, qui innumerabilis mundos infinitasque regiones, quarum nulla esset ora, nulla extremitas, mente peragravisset.
Illud non continuo, ut aeque incontentae. Eiuro, inquit adridens, iniquum, hac quidem de re; Haec bene dicuntur, nec ego repugno, sed inter sese ipsa pugnant.
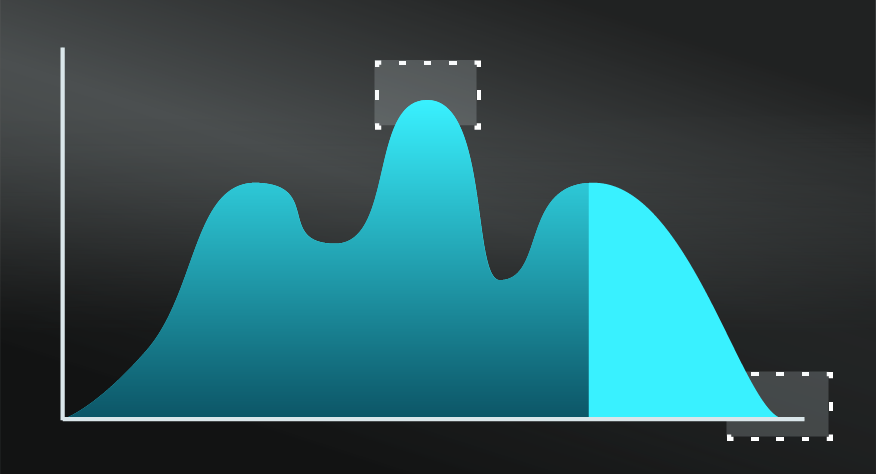
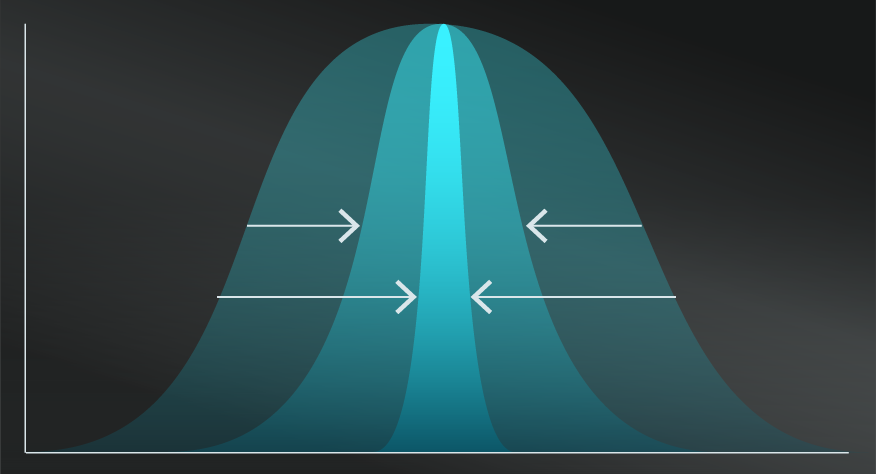
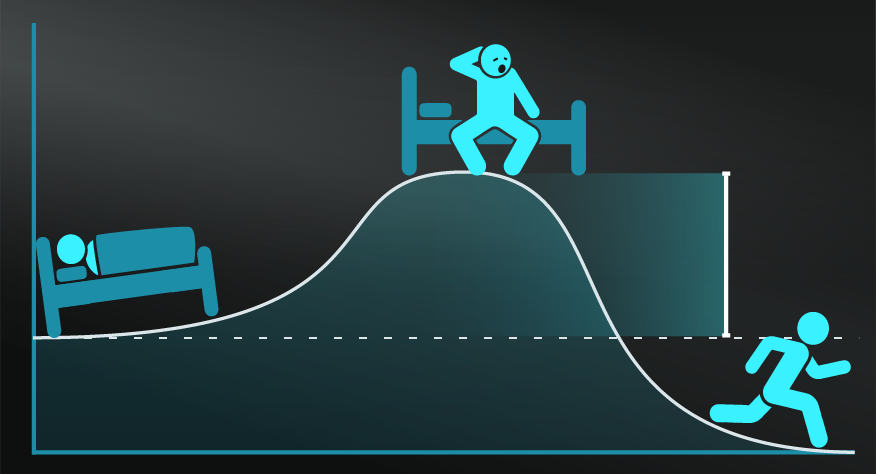
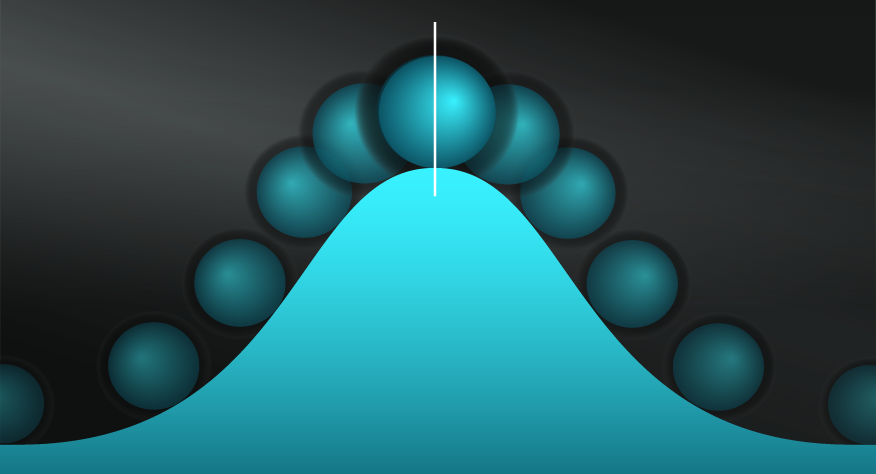
- Find the optimal peak.
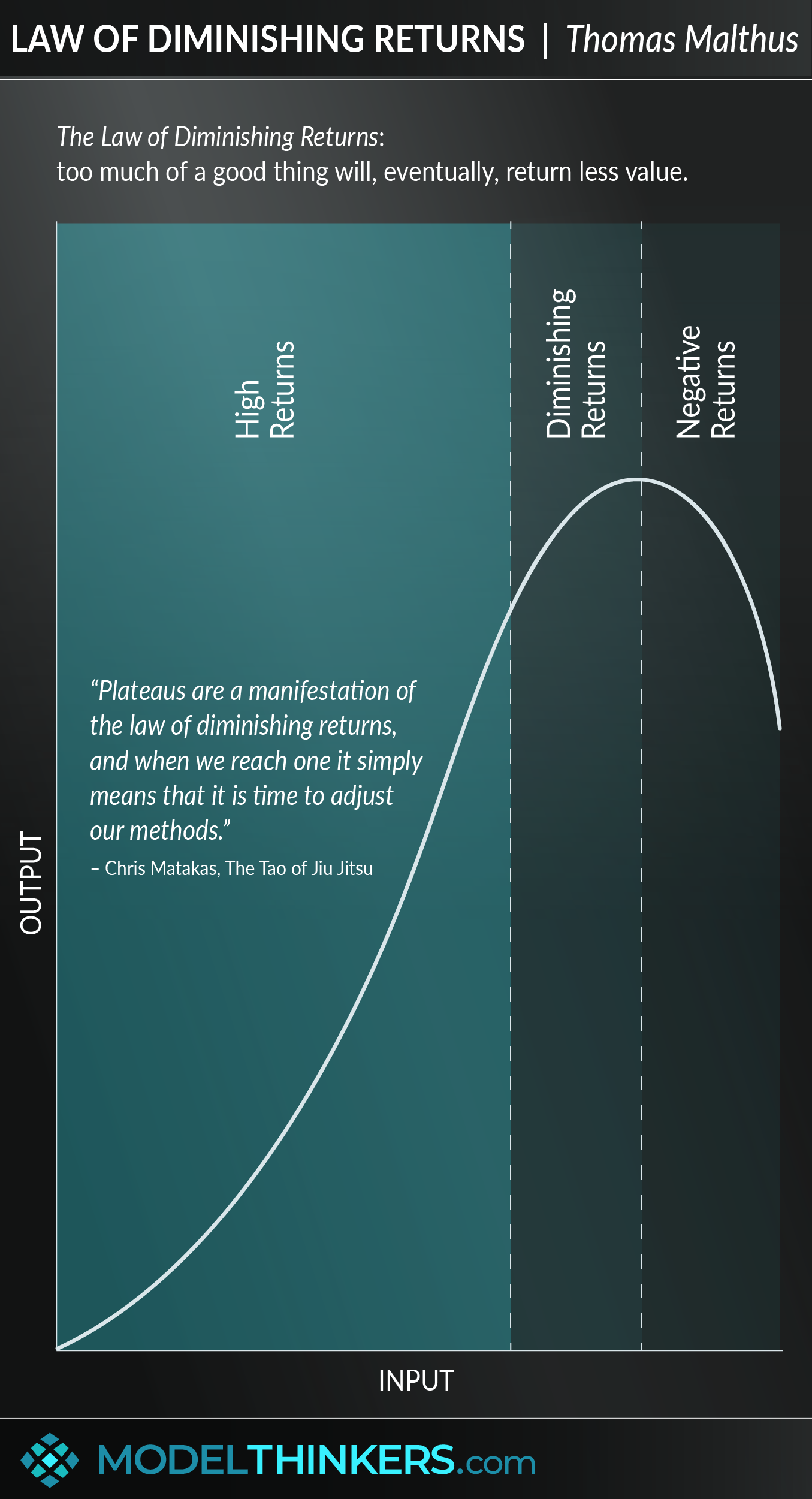
Know that ‘more of a good thing is not always better’ ...
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Quamvis enim depravatae non sint, pravae tamen esse possunt. Tertium autem omnibus aut maximis rebus iis, quae secundum naturam sint, fruentem vivere. Duo Reges: constructio interrete. Quid de Pythagora? Illud dico, ea, quae dicat, praeclare inter se cohaerere. Ego vero isti, inquam, permitto.
Iam id ipsum absurdum, maximum malum neglegi. Aut haec tibi, Torquate, sunt vituperanda aut patrocinium voluptatis repudiandum. Est autem a te semper dictum nec gaudere quemquam nisi propter corpus nec dolere. Tum Piso: Quoniam igitur aliquid omnes, quid Lucius noster? Quem ad modum quis ambulet, sedeat, qui ductus oris, qui vultus in quoque sit? In eo autem voluptas omnium Latine loquentium more ponitur, cum percipitur ea, quae sensum aliquem moveat, iucunditas. Ita relinquet duas, de quibus etiam atque etiam consideret. Quo minus animus a se ipse dissidens secumque discordans gustare partem ullam liquidae voluptatis et liberae potest. Non igitur de improbo, sed de callido improbo quaerimus, qualis Q.
Inquit, dasne adolescenti veniam? Tum, Quintus et Pomponius cum idem se velle dixissent, Piso exorsus est. Modo etiam paulum ad dexteram de via declinavi, ut ad Pericli sepulcrum accederem. Mihi, inquam, qui te id ipsum rogavi? Ita multo sanguine profuso in laetitia et in victoria est mortuus.
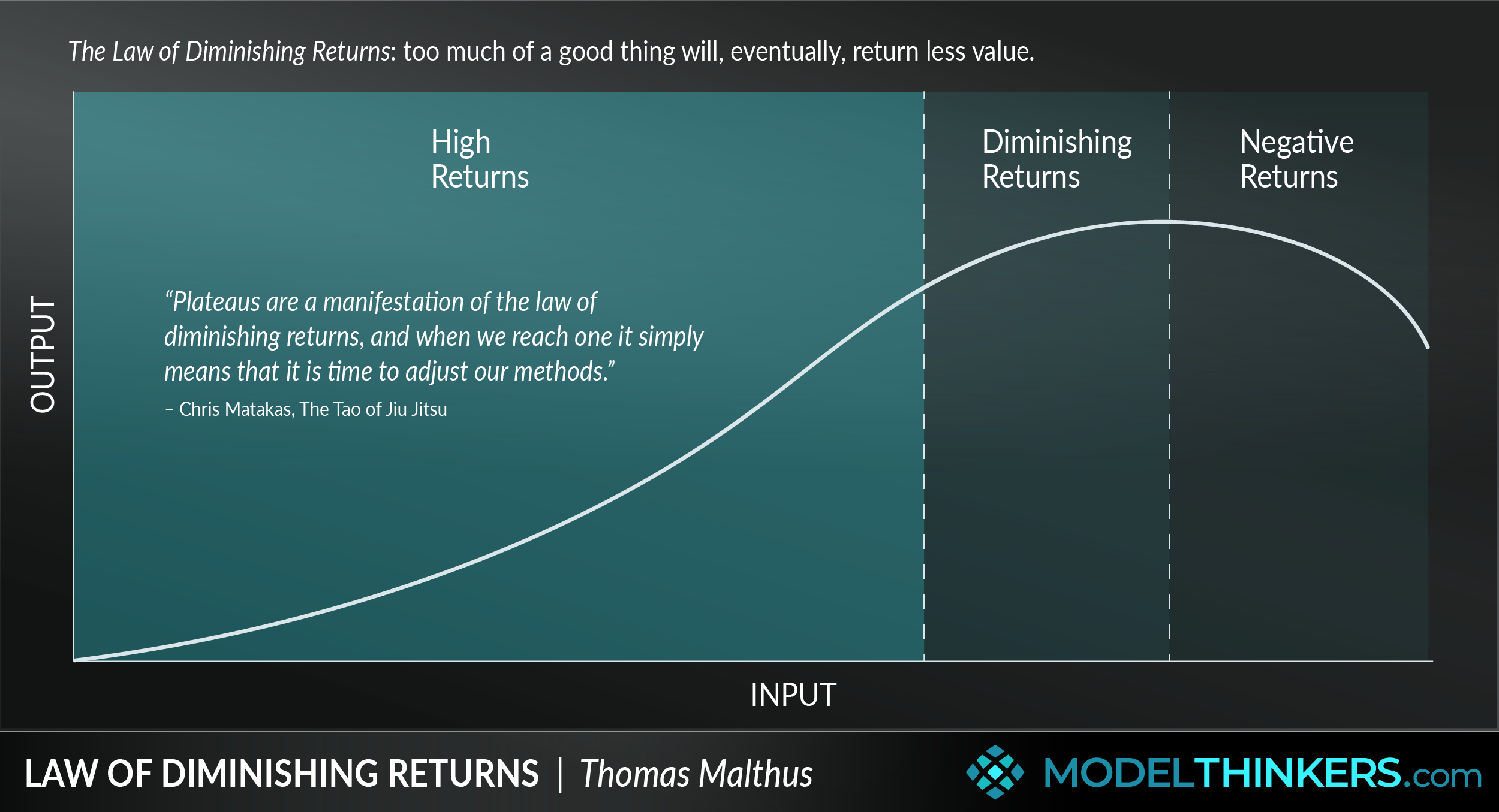
The Law of Diminishing Returns is based on a number of assumptions that are not always relevant to real-world situations. These include:
-
No change in technology
-
A short period of impact
-
Consistent, homogeneous units
-
Measurement of product using tangible units.
Each of these assumptions might be challenged in the real world. Technology is always progressing, the units of input are likely going to vary (hiring one person compared to another person will have different impacts) and even the questions of measurement will be more complex beyond the narrow assessment of weight or financial value.
It relies on a static, predictable system which is rarely true or at least has clear limitations when applied to the complexity of reality.
Too Many Cooks.
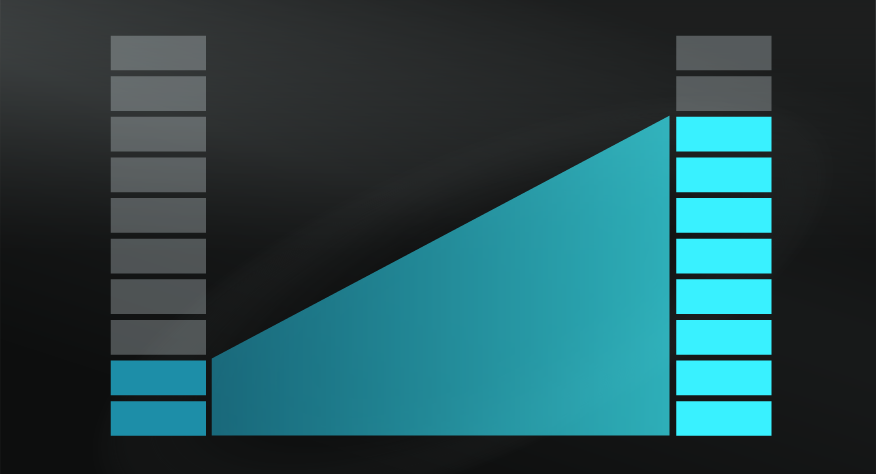
A useful example to explain this model is to consider a small food truck that sells doughnuts. If that truck has one cook, they might be able to produce 20 doughnuts every hour. Adding one more cook might increase that output to 40 doughnuts every hour. However, adding a third cook might only allow them to produce 45 doughnuts every hour because of the limited space and resources in the truck, and adding a fourth cook might not add any returns at all.
d
The concept of Diminishing Returns has a rich and long history, being traced back to economists such as Adam Smith, Jacques Turgot, and Thomas Mathus. The earliest explicit references to this model were in relation to farming outputs and can be attributed to Thomas Malthus and David Ricardo.
My Notes
Oops, That’s Members’ Only!
Fortunately, it only costs US$5/month to Join ModelThinkers and access everything so that you can rapidly discover, learn, and apply the world’s most powerful ideas.
ModelThinkers membership at a glance:
“Yeah, we hate pop ups too. But we wanted to let you know that, with ModelThinkers, we’re making it easier for you to adapt, innovate and create value. We hope you’ll join us and the growing community of ModelThinkers today.”
You Might Also Like:
- Actionable summaries of the world's most powerful ideas.
Subscribe now and download this practical guide to transform your thinking, plus recieve one short, powerful and actionable idea in your inbox each month.